Contour Lines are rows of trees planted level along a hill's contour They intersect rainwater runoff, trap eroding soil, and build terraces of fertility over time Work, not words Our broader purpose is to extend the ecological mindset, to promote reforestation and regenerative agricultureInstead, we can look at the level sets where the function is constant For a function of two variables, above, we saw that a level set was a curve in two dimensions that we called a level curve For a function of three variables, a level set is a surface in threedimensional space that we will call a levelIf a Model is exported with quick draw contours turned on, then each triangles contours are output as single short straight lines Threaded These are final presentation quality contours that can be curved and broken to have level text inserted into them
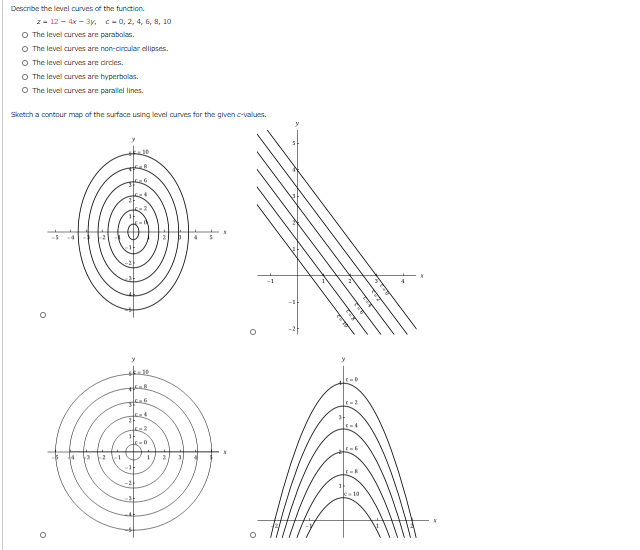
Describe The Level Curves Of The Function Z 12 4x Chegg Com
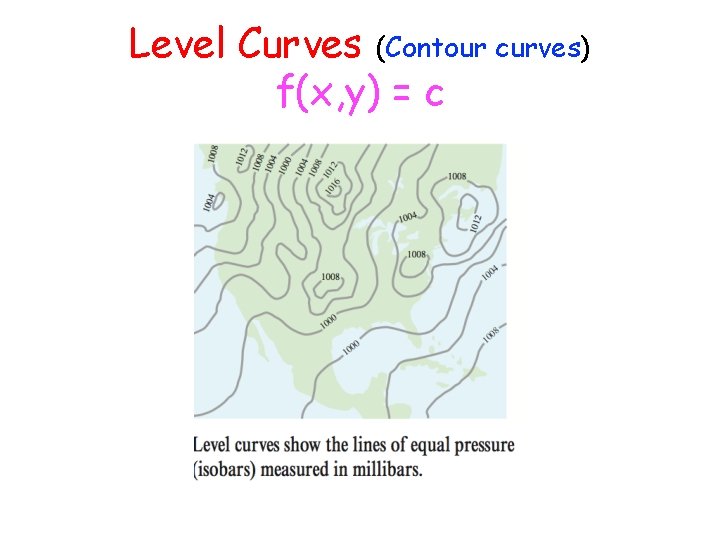
Level curves and contour lines
Level curves and contour lines-By combining the level curves f (x, y) = c for equally spaced values of c into one figure, say c = − 1, 0, 1, 2, , in the x y plane, we obtain a contour map of the graph of z = f (x, y) Thus the graph of z = f (x, y) can be visualized in two ways, one as a surface in 3 space, the graph of z = f (x, y),ColorFunction is supplied with a single argument, given by default by the average of the scaled values of f for each pair of successive contour levels With the default settings Exclusions>Automatic and ExclusionsStyle>None, ContourPlot breaks continuity in its sampling at any discontinuity curve it detects The discontinuity is immediately visible only if it jumps out of a particular contour level




Lagrange Multipliers
You can change which values the contour lines should display by tweaking the "Range of contour levels" and "Number of contour levels" sliders By default they are set to (100,100) and 21 respectively, so this means that the displayed contour levels will start at 100 and go up to and including 100 in intervals of Contour lines are imaginary lines that connect places at the same height above sea level These are recorded in brown on the survey maps These documents appear to be closed curves The height difference between the two adjacent contour lines on the survey map is m This is called contour intervalThese maps are marked with contour lines or curves connecting Topographic (also called contour) maps are an effective way to show the elevation in 2D maps These maps are marked with contour lines or curves connecting The level curves are parallel lines of the form \2xy1=c\ The graph and some level curves are drawn in Figure 5
Then the projection of the set of level curves of $f$ onto the $xy$plane is called the Contour Plot or Contour Map of $f$ When we depict a contour plot of a two variable function, it is important to note that it is impossibly to place all the level curves of $z = f(x, y)$ onto the $xy$ plane, and so we often choose specific level curvesLevel curves are in the xy plane One level curve consists eg of all (x,y) points which satisfy f(x,y)=100 If , then this level curve will be the circle Another level curve will be the circle , etc A contourplot is a 2d representation of a 3d surface, just like a flat (ie, 2d) map is a representation of the 3d mountainsGraphs of Surfaces and Contour Diagrams 3 Together they usually constitute a curve or a set of curves called the contour or level curve for that value In principle, there is a contour through every point In practice, just a few of them are shown The following is the contour diagram for the earlier surface 0 0 0 0 0 0 0 2 2
A contour line is a curve that joins points of equal value In cartography, contour lines join the points of equal elevation above a given standard level like the mean sea level A contour map is a map to illustrate the topographical features of an area using contour lines It is often used to show the heights, slopes and depths of valleys andPut simply, contour lines mark points of equal elevation on a map If you trace the length of a line with your finger, each point you touch is the same height above sea level If you were to walk the path of a contour line in real life, you would remain at the same elevation the whole hike, never traveling up or downIf you're looking at a contour plot where the intervals between level curves are at regular distances, then very close contour lines means that the function is very steep there So that's something to keep in mind Let's look at one more example This is z equals x squared minus y squared



Level Curves And Contour Plots Mathonline



1
Level sets show up in many applications, often under different names For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit equationAnalogously, a level surface is sometimes called an implicit surface or an isosurface The name isocontour is also used, which means a contour ofIn other words, these commands both produce a set of level curves of the input function for a discrete set of values (ie levels) of the third coordinate The differences are as follows contourplot3d generates a 3D view of the contours raised to their appropriate levels, whereas contourplot generates a flat 2D contourContourf (z) contourf (z, vn) contourf (x, y, z) contourf (x, y, z, vn) contourf (, style) contourf (hax, ) c, h = contourf () Create a 2D contour plot with filled intervals Plot level curves (contour lines) of the matrix z and fill the region between lines with colors from the current colormap The level curves are taken from the contour matrix c computed by contourc for




Contour Plot An Overview Sciencedirect Topics




Describe The Level Curves Of The Function Z X2 Chegg Com
Contour lines are very popular among cartographers as they provide a picture of the 3D terrain using only a planar map Irregular triangulations are most suitable for 3D visualization because the current 3D visualization is based on triangles Level curves may be obtained directly or computed as the isolines of a surface fitting the initial dataLabel spacing along the contour lines, specified as a scalar value in points, where one point is 1/72 inch Use this property to control the number of contour labels along the contour lines Smaller values produce more labels You must set the ShowText property to 'on' for the LabelSpacing property to have an effectLevel curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plot Example To illustrate this we first draw the graph of z = x2 y2 On this graph we draw contours, which are curves at a fixed height z = constant For example the curve at height z = 1 is the circle x2 y2 = 1 On the graph we have



Graph A Contour Plots Level Curves Using 3d Calc Plotter Youtube



Http Academic Brcc Edu Ryanl Modules Multivariable Traces Traces Pdf
Contour plot is a collection of contour lines Each contour is a curve that is a resultant of cutting a surface by a plane Every contour need not form a curve Some of the resultant contours can be a straight line as well Here is the formal definition of a contour plot A level curve of a function f (x,y) is the curve of points (x,y) where fA contour line (also known as a level curve) for a given surface is the curve of intersection of the surface with a horizontal plane, z = c A representative collection of contour lines, projected onto the xyplane, is a contourThe projection of the contour line at height c into the xyplane is called the level curve at level c Thus a level curve is a plane curve Since the level curves of a function are implicitly defined plane curves, they can be drawn with the use of implicitplot But a




Livro E Resolucao Do Livro De Calculo De Gilbert Strang Mit 33 Livro E Resolucao Docsity




13 1 Day 2 Level Curves Level Curves One Way To Visualize A Function Of Two Variables Is To Use A Scalar Field In Which The Scalar Z F X Y Is Assigned
Given a vertical direction, the contour lines (or curves) of a surface (S) are the sections of this surface by the horizontal planes (ie perpendicular to the vertical direction) Remark the projections on the plane xOy of the contour lines of the surface , are the curves solution of the differential equation (where );LEVEL CURVES The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant;33 Representation with contour lines an algorithm problem Although determining the color of a pixel by interpolation is easy, constructing the contour lines sensu stricto is more difficult Indeed, a contour line is an equation curve f(x, y) = C k, with C k being the kth level




Graph And Contour Plots Of Functions Of Two Variables Wolfram Demonstrations Project



Contour Plot Under Surface Plot Matlab Surfc
What is Contour line in Surveying ?Google Maps added the highlight option to the map display, which includes contour lines from a certain zoom level This is activated in the left panel «Relief» and in the floating button you can activate or deactivate the curve view I am trying to plot contour lines of pressure level I am using a netCDF file which contain the higher resolution data (ranges from 3 km to 27 km) Due to higher resolution data set, I get lot of pressure values which are not required to be plotted (rather I don't mind omitting certain contour line of insignificant values)



Albania And The Disease Of Level Curves Der Elefant Kommt Mit




Draw A Contour Map Of The Function Showing Several Level Curves F X Y Sqrt X Y Study Com
Free ebook http//tinyurlcom/EngMathYT How to sketch level curves and their relationship with surfaces Such ideas are seen in university mathematics and Now to make it perfect, I would only need to add the lines to show the contour of the graph, more specifically the likes of x^2 4*y^2 = 1 and x^2 4*y^2 = 2 Now this is where I am stuck and don't know how to do it It should look something like this thoughA Contour line may be defined as an imaginary line passing through the points of equal devotion A contour line may also be defined as the intersection of a level surface with the surface of the earth When the contours are drawn underwater, they are termed as Submarine Contours, Fathoms or Bathymetric Curves



Contour Lines Rodolphe Vaillant S Homepage




Help Online Origin Help Creating Contour Graphs
Problem with level curves patch and topography I've used ArcMap with a DEM (Digital Elevation Model) to produce contour lines from a region of 10km x 10km approx I have performed a smooth line to have nice smooth contour lines that I've imported into Rhino for further modeling The model is scaled down in Rhino at 125 000 to have a modelGiven a functionf(x, y), the setf(x, y) =c= const is called acontour curveorlevel curve off For example, forf(x, y) = 4x2 3y2the level curvesf=care ellipses ifc >0 Level curves allow to visualize functions of two variablesf(x, y) ExampleForf(x, y) =x2−y2Therefore, they are the equipotential lines of the vector field ;



Contour Map Of The Function Showing Several Level Curves Physics Forums



Level Curves And Contour Plots Mathonline
A contour plot can be created with the pltcontour function It takes three arguments a grid of x values, a grid of y values, and a grid of z values The x and y values represent positions on the plot, and the z values will be represented by the contour levels Perhaps the most straightforward way to prepare such data is to use the npmeshgrid function, which builds twodimensional grids fromCreating Level Curves Turn off all the layers you do not want to see at the moment Configure contour features by selecting contour / contour properties and enable the following options Now we create the curves with the option contour / create contour Plot contour lines Call signature contour( X, Y, Z, levels, **kwargs) contour and contourf draw contour lines and filled contours, respectively Except as noted, function signatures and return values are the same for both versions Parameters X, Yarraylike, optional The coordinates of the values in Z




Graph And Contour Plots Of Functions Of Two Variables Wolfram Demonstrations Project



1
Ie the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the function The next topic that we should look at is that of level curves or contour curves The level curves of the function z = f (x,y) z = f (x, y) are two dimensional curves we get by setting z = k z = k, where k k is any number So the equations of the level curves are f (x,y) = k f (x, y) = k A contour is a line drawn on a map that joins points of equal height above sea level For 125 000 scale maps the interval between contours is usually 5 metres, although in mountainous regions it may be 10 metres How contour lines show a pair of small hills




Level Sets Math Insight




Contour Maps In Python
When we move perpendicularly to the contour line, that direction changes f (x, y) the fastest, so it's the gradient Remember we're taking derivatives of the entire function, not just the function restricted to the contour lines (in which case, yes, it's a constant) Hope this helps!Ask Question Asked 6 years ago Active 6 years ago Viewed 543 times 0 $\begingroup$ But I don't quite know how to use this knowledge to sketch the level curves of f calculus Share Cite Follow edited Jun 1Points with the same elevation are joined by lines You have seen weather maps where points with equal temperature are joined by lines (these lines are called isotherms) A contour plot of the function z=f(x,y) consists of a family of curves f(x,y)=c (called level or contour curves) in the xy plane for various values of c On the curve f(x,y)=c




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Level Curves Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
The level curves (or contour lines) of a surface are paths along which the values of z = f (x,y) are constant; Yes, I meant by 'contour line' a line on which $f$ is constant However, I now realized that I should refer to such a line as 'level curve' since 'contour line' may mean any line on a 2 or higher dimensional space About the saddle, I was thinking it as an isolated pointADVERTISEMENTS After reading this article you will learn about 1 Definition of Contour 2 Contour Interval and Horizontal Equivalent 3 Characteristics 4 Methods 5 Interpolation 6 Drawing the Contour Lines Definition of Contour A contour or a contour line may be defined as the line of intersection of a level surface with the surface of



Level Curves Or Contour Curves Youtube




Draw A Contour Map Of The Function Showing Several Level Curves F X Y Y X 2 Y 2 Youtube
Direct link to Kunal Muley's post "At 241 in the video we see that the contour lines" in the video we see that the contour lines for z=1, not intersecting at point (0,0) in the XY plane in the video, Grant marks a contour line as z=1 which intersects at pint (0,0) in the XY plane Sketch the level curves (contour lines) of the function?Ie the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves



Functions Of Several Variables Ximera



How To Make A Contour Plot In Python Using Bokeh Or Other Libs Stack Overflow
A contour line of a function of two variables is a curve along which the function has a constant value, so that the curve joins points of equal value It is a plane section of the threedimensional graph of the function f parallel to the plane In cartography, a contour line joins points of equal elevation above a given level, such as mean sea level A contour map is a map illustrated with(D) The horizontal distance between two points on same contour Answer Option A 13 Check lines (or proof lines) in Chain Surveying, are essentially required (A) To plot the chain lines (B) To plot the offsets To indicate the accuracy of the survey work (D) To increase the outturn Answer Option C 14




Find And Sketch The Level Curves F X Y C On The Same Set Of Coordinates Axes For The Given Values Of Brainly Com




Contour Plots Video Khan Academy



Help Online Tutorials Contour Plots And Color Mapping




Topographic Lines Stock Illustrations 5 478 Topographic Lines Stock Illustrations Vectors Clipart Dreamstime




What Is A Contour Plot Or A Contour Figure How Are They Formulated And What Are Their Applications Quora



Contour Line Wikipedia



Level Curves And Contour Plots
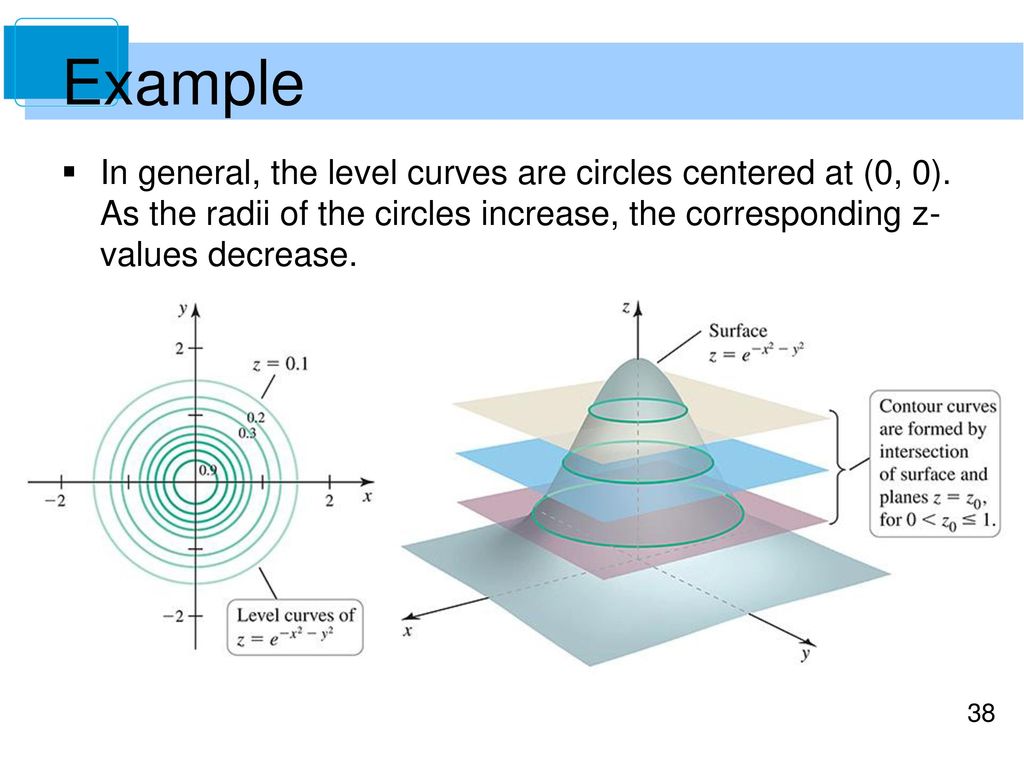



Introduction To Functions Of Several Variables Ppt Download



Vb Helper Howto Draw Contour Plots Level Curves For A Function With Known Derivatives



1




14 8 Lagrange Multipliers Mathematics Libretexts




Using 2d Contour Plots Within Ggplot2 To Visualize Relationships Between Three Variables R Bloggers




Describe The Level Curves Of The Function Z 12 4x Chegg Com




Level Sets Math Insight




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
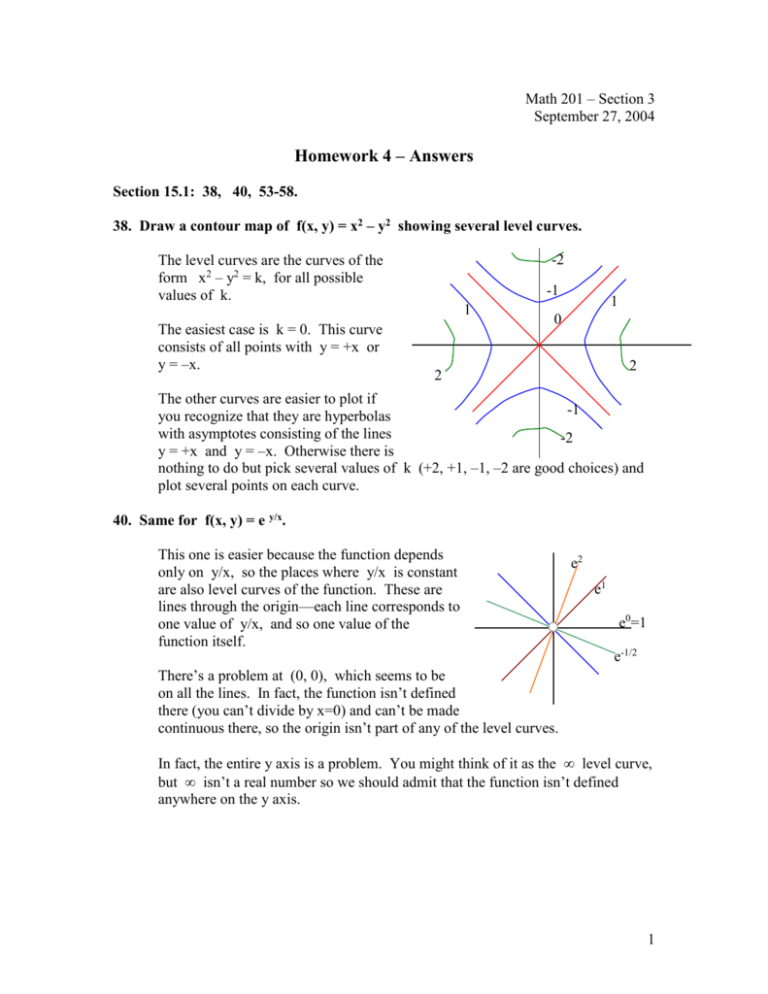



Answers To Homework 4




Calculus Iii Functions Of Several Variables




Locus Of Osculation For Two Families Of Ellipsoidal Level Curves Download Scientific Diagram




14 Partial Derivatives Copyright Cengage Learning All Rights




Level Set Examples Math Insight




Level Curves Of Functions Of Two Variables Youtube



Contour Plots Geogebra
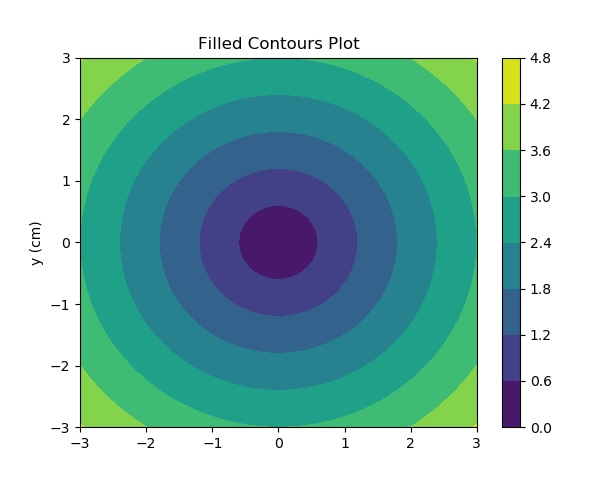



Matplotlib Contour Plot Tutorialspoint




Level Curves




Maple Tutor Part 11



Contour Plots Definition Examples Statistics How To




Level Set Wikipedia



Contour Lines Rodolphe Vaillant S Homepage
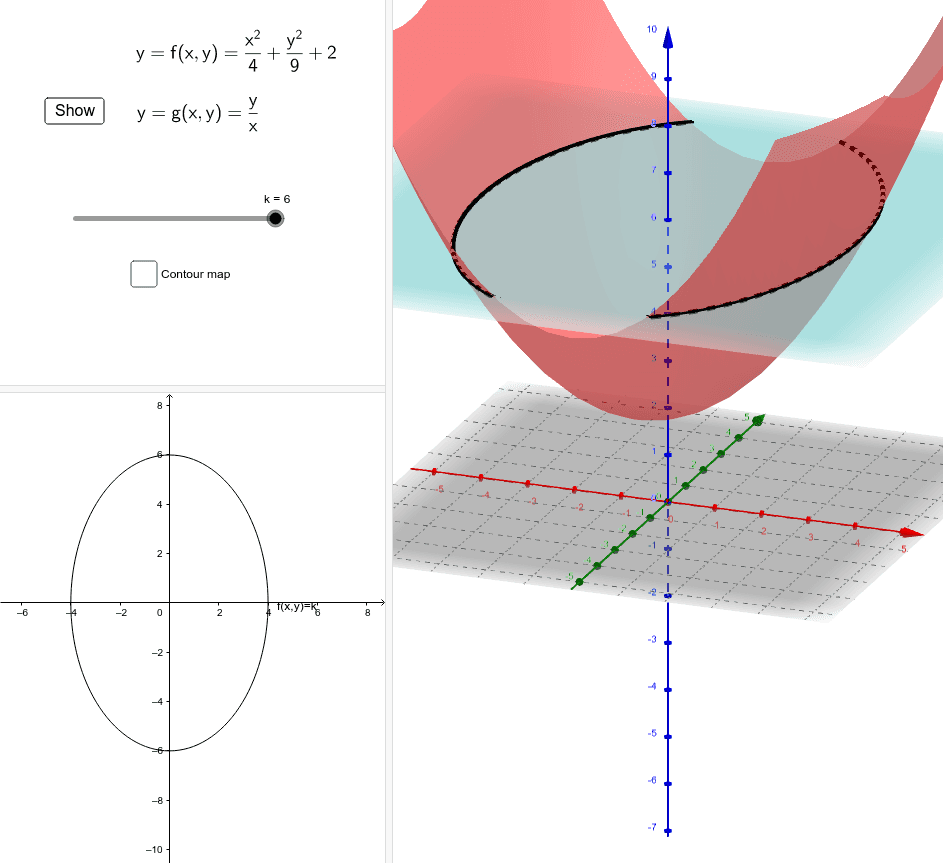



Level Curves Masolata Geogebra




Level Curves




Level Curves And Contour Maps Calculus 3 Youtube




Level Curves
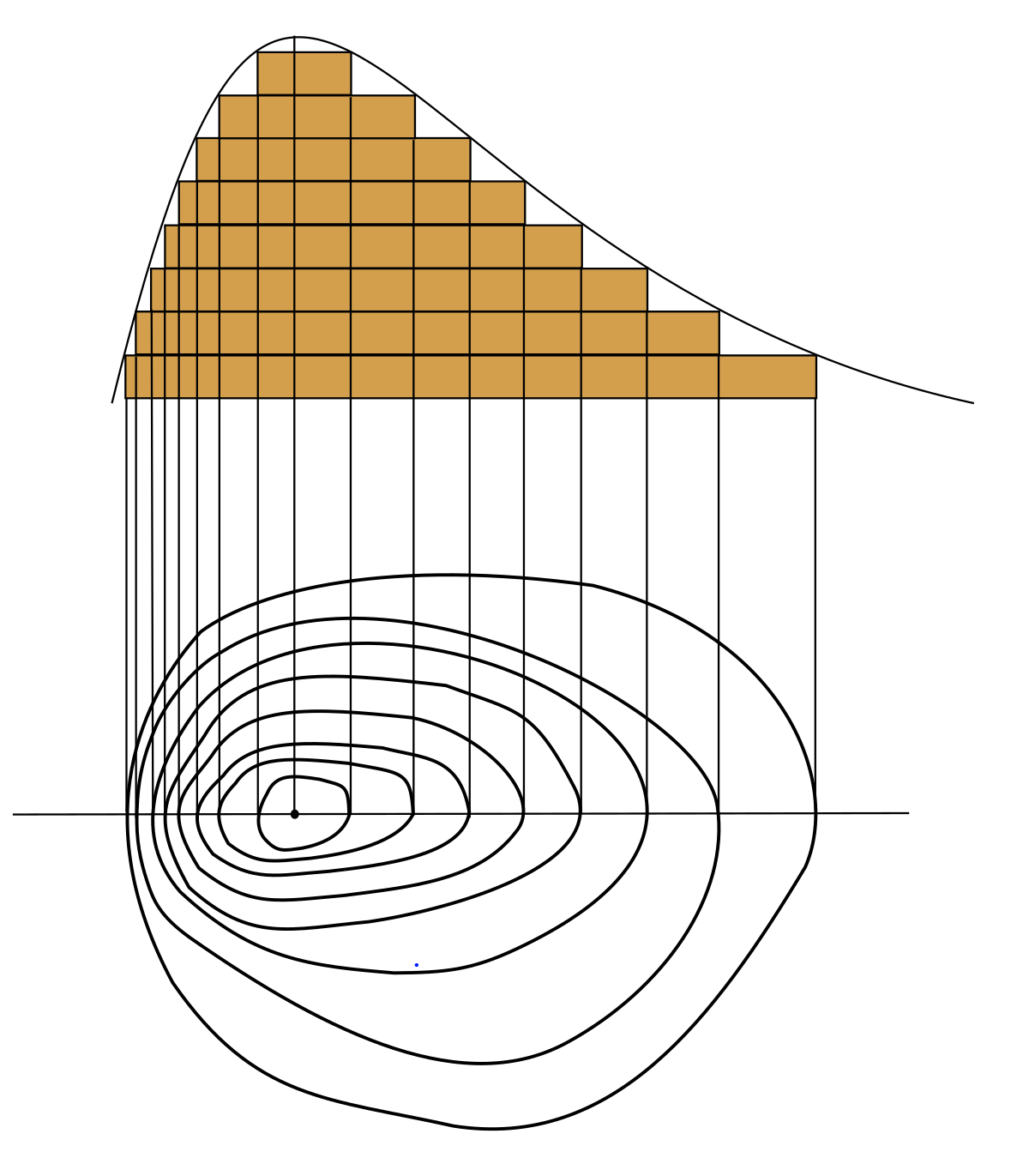



Contour Line Wikipedia




Level Sets Math Insight




Contour Lines Of The Zeta Function Z S Of A Random Complex In This Download Scientific Diagram



Level Curves And Contour Plots Mathonline
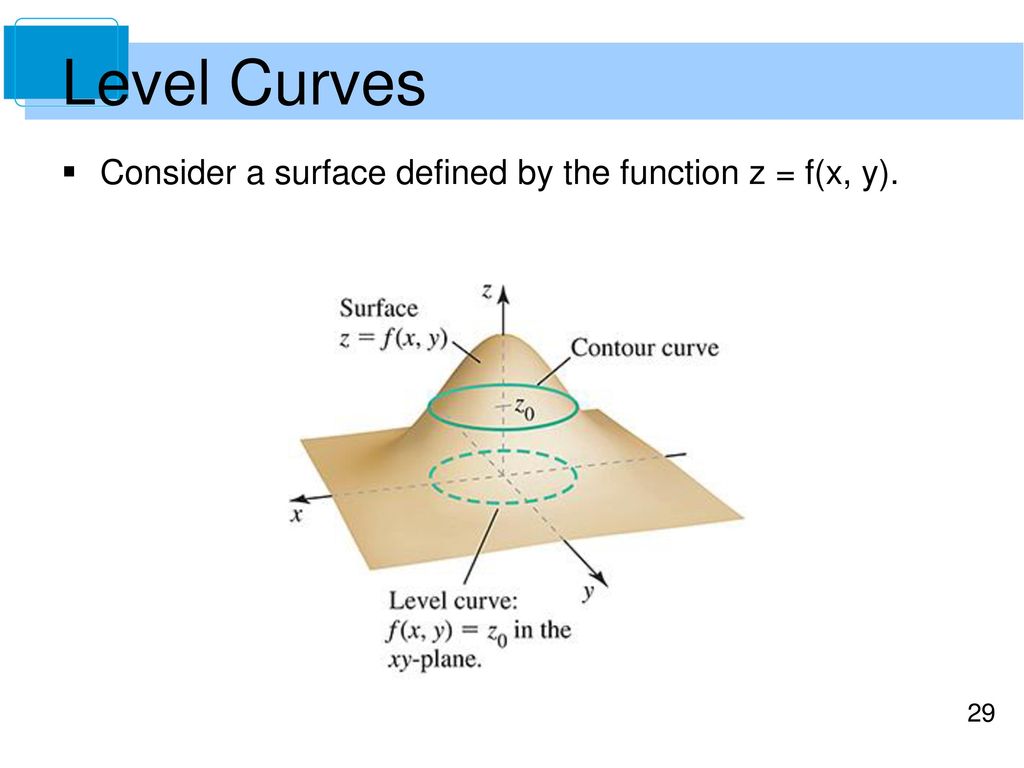



Introduction To Functions Of Several Variables Ppt Download




Lagrange Multipliers



Level Curves And Contour Plots Mathonline



1




How To Sketch Level Curves Youtube
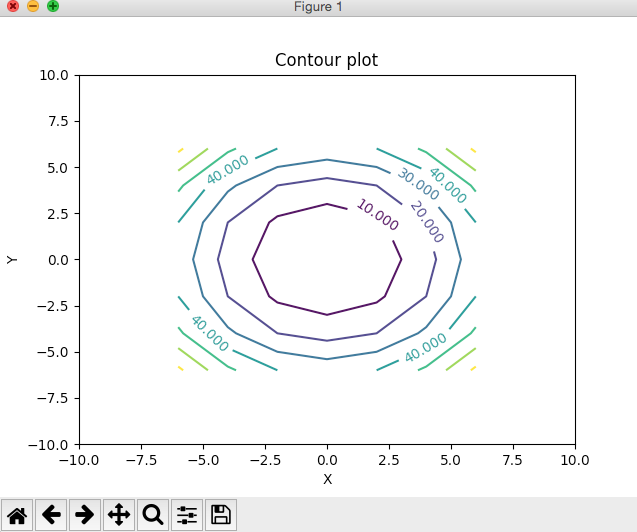



Contour Plot Using Python And Matplotlib Pythontic Com




Matlab Tutorial



Contour Plots In Excel How To Create Contour Plots In Excel




Level Curves Contours Of Arrokoth Topographic The Color Bar Denotes Download Scientific Diagram




Function Reference Contour
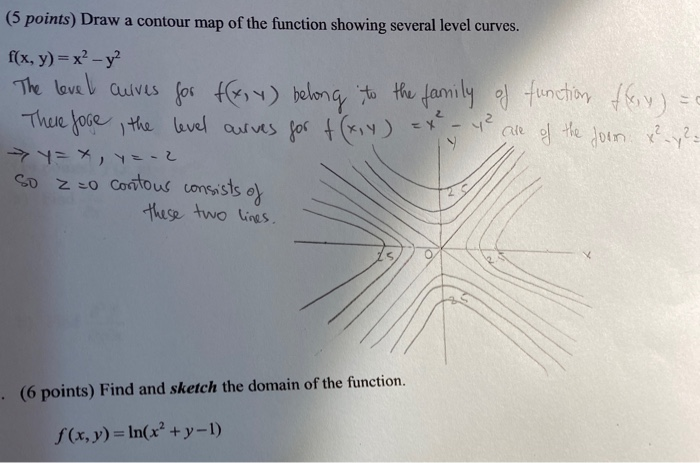



5 Points Draw A Contour Map Of The Function Showing Chegg Com
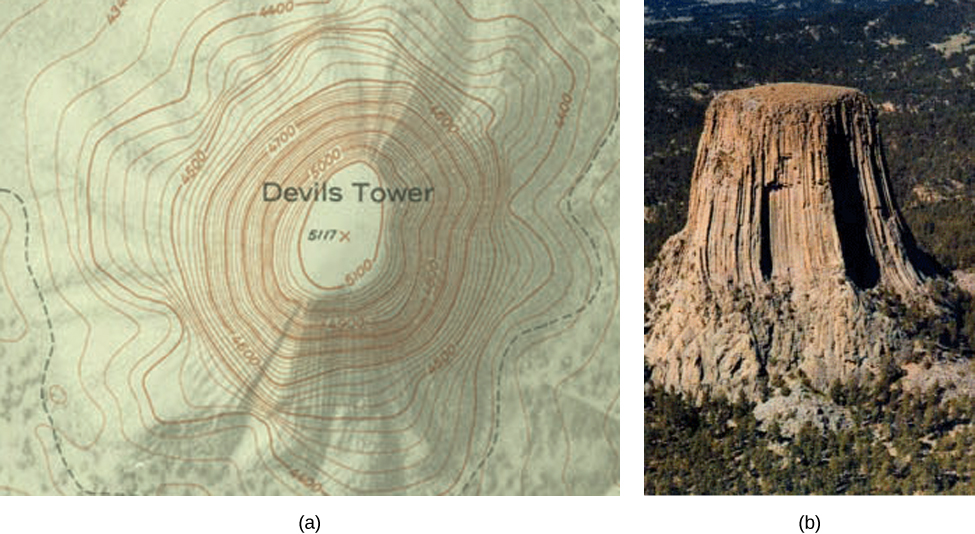



Level Curves Functions Of Several Variables By Openstax Page 3 12 Jobilize




Calculus Iii Functions Of Several Variables
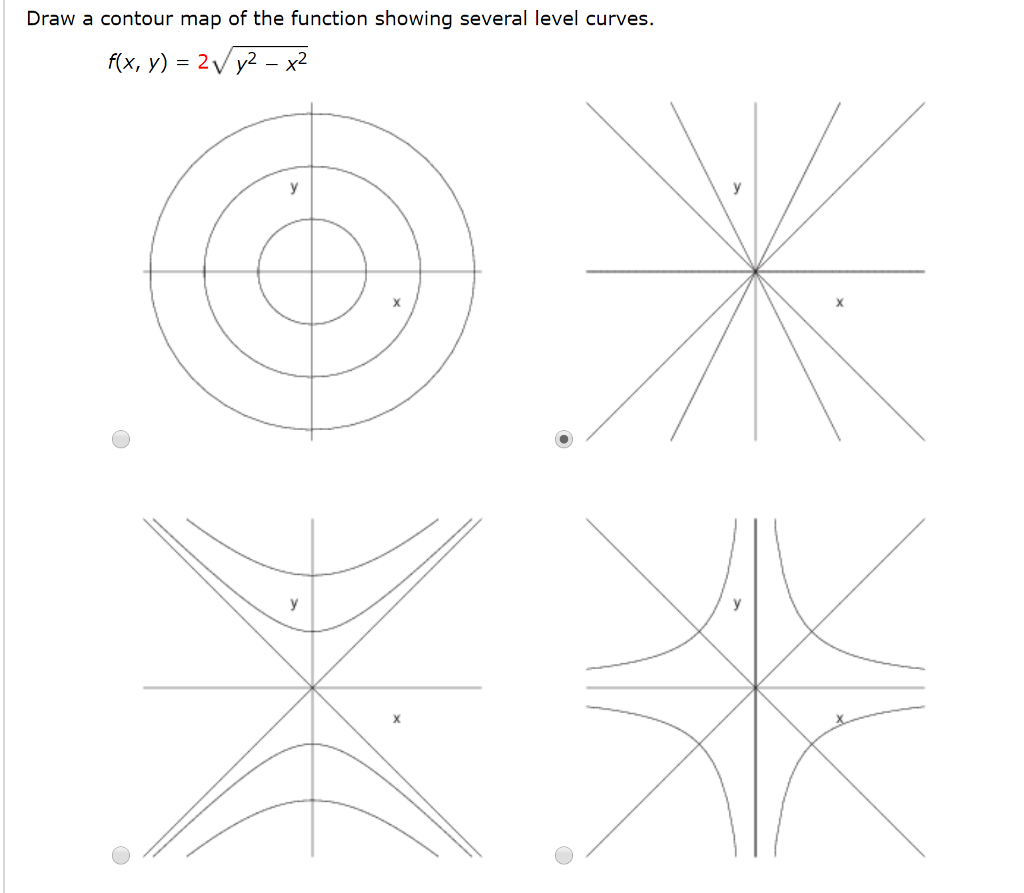



Draw A Contour Map Of The Function Showing Several Chegg Com
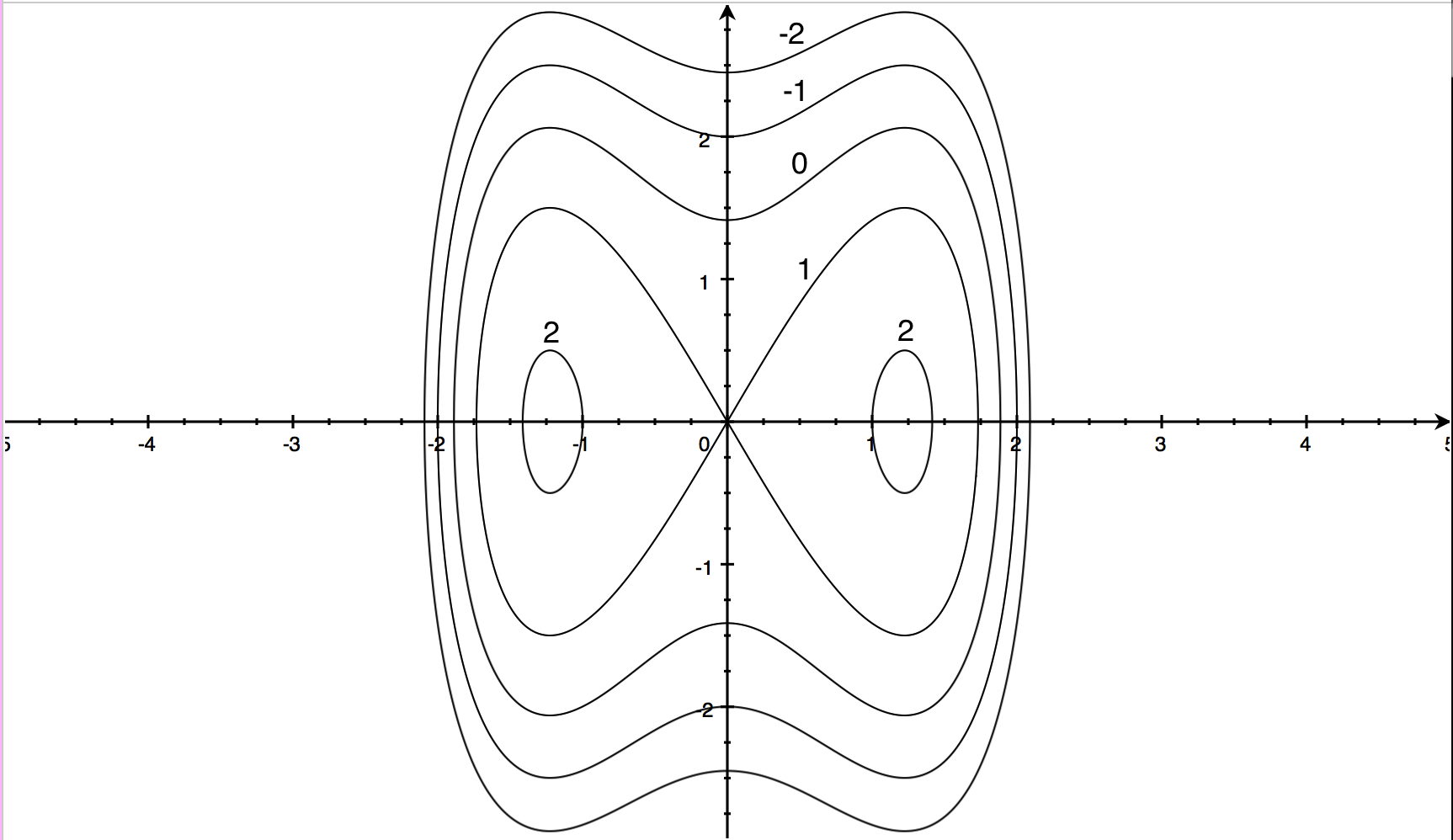



Contour Maps Article Khan Academy



Contour Curves Options




Draw A Contour Map Of The Function Showing Several Chegg Com
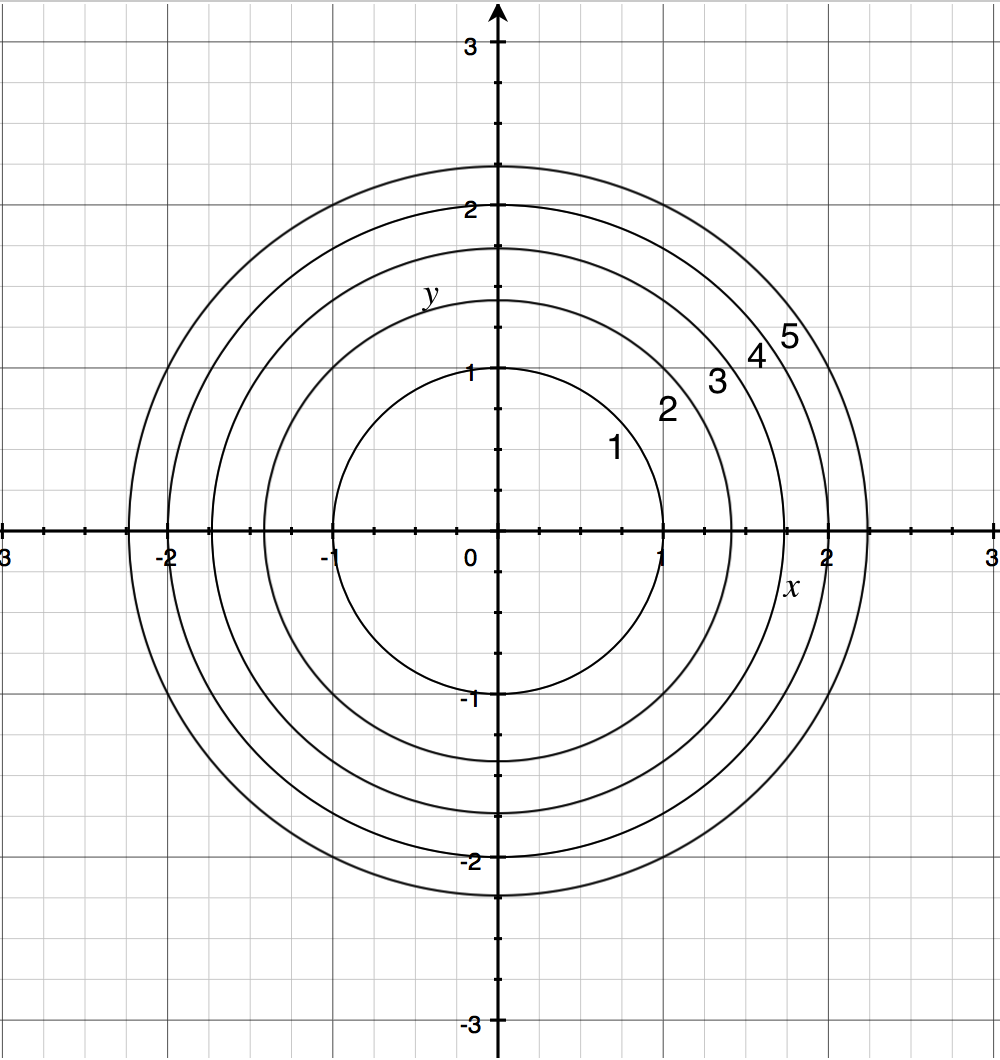



Contour Maps Article Khan Academy
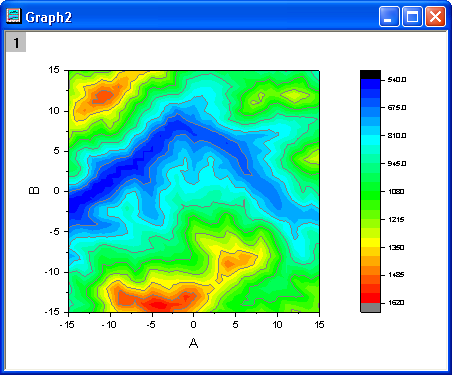



Help Online Tutorials Contour Plots And Color Mapping



Contour Lines Rodolphe Vaillant S Homepage
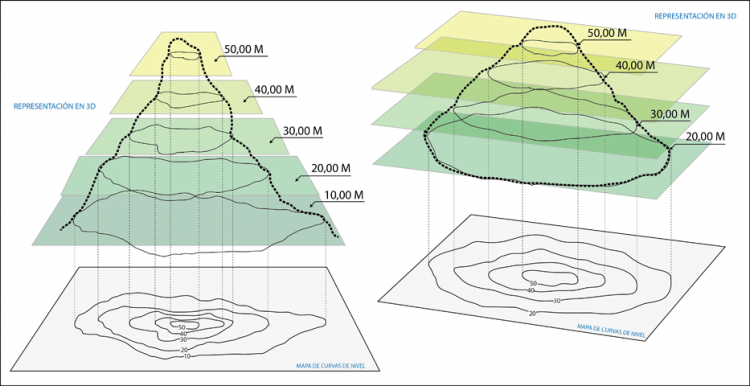



Building Elevation And Topographical Maps Using Deep Learning



Level Curves And Contour Plots Mathonline




Gradient Of 0 Novocom Top




Draw A Contour Map Of The Function Showing Several Chegg Com




How To Visualize Gradient Descent Using Contour Plot In Python




Finding Extrema Non Critical Points And Saddle Points Given A Contour Plot Mathematics Stack Exchange




11 Level Curves And Contour Lines Of Functions Of Two Variables Youtube




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



12 1 Introduction To Multivariable Functions Mathematics Libretexts



Contour Lines Or Level Curves




Level Curves For The Region Of The Potential Energy Surface With The Download Scientific Diagram



Contour Lines Rodolphe Vaillant S Homepage




Level Curves
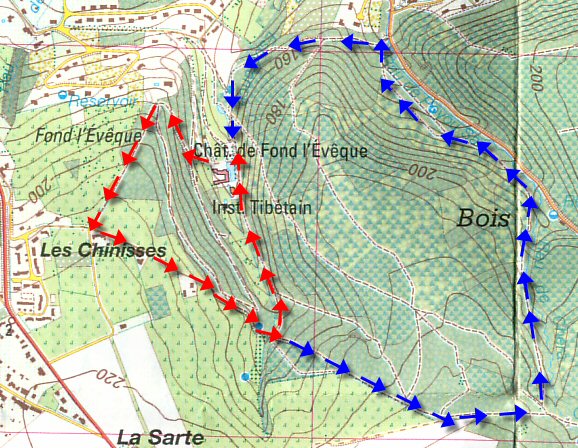



Extra Explanation Wiskunde Op Tilburg University




Sketch A Contour Diagram Of Each Function Then Decide Whether Its Contours A Predominantly Lines Parabolas Ellipses Or Hyperbola 1 Z 4x2 2 Z X2 4y2 3 Z
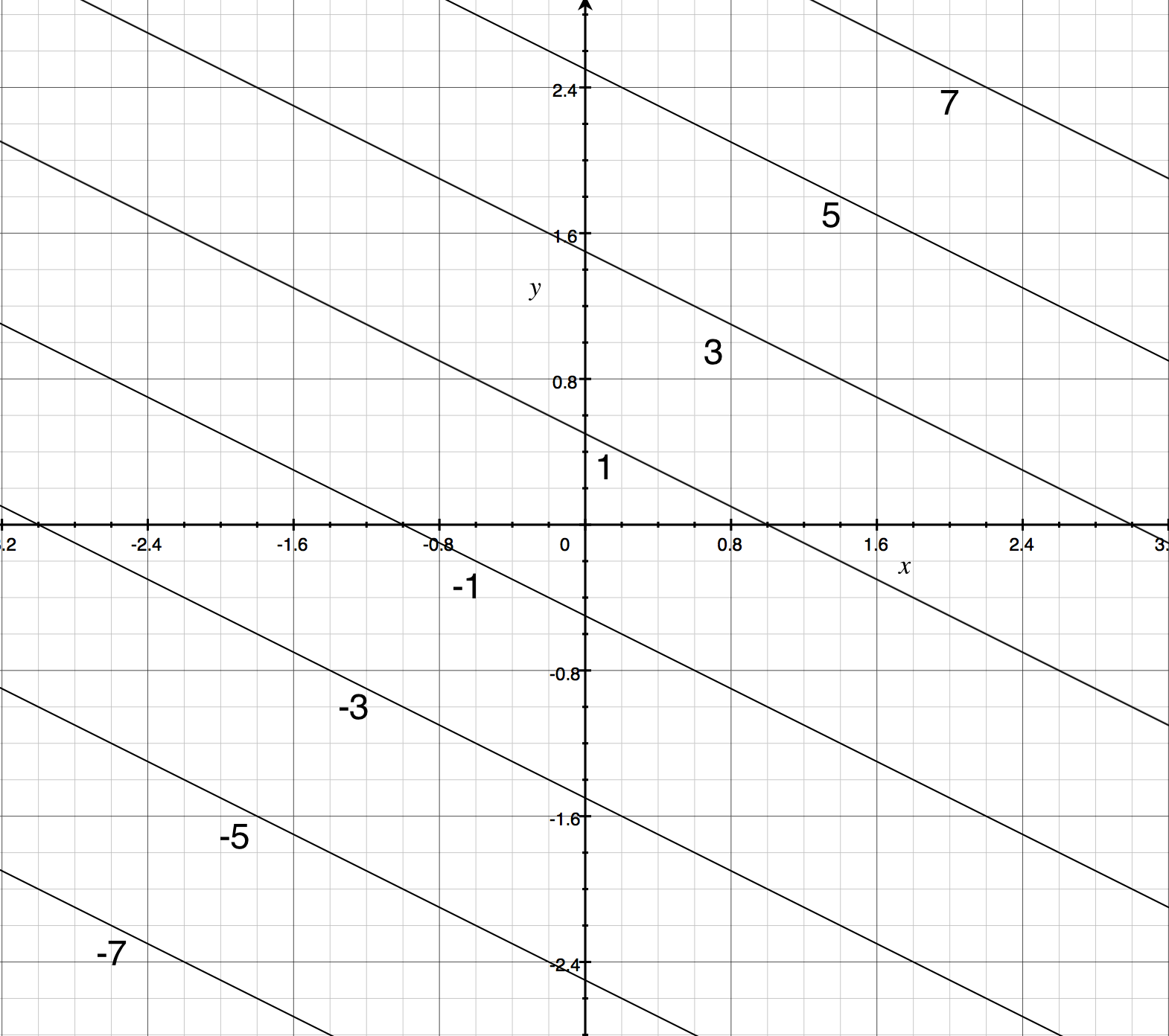



Contour Maps Article Khan Academy
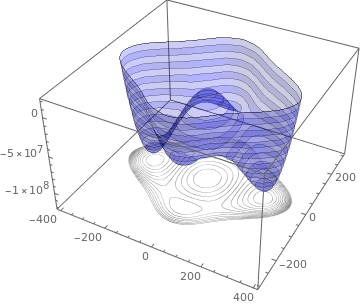



Functions Of Several Variables Ximera




Draw A Contour Map Of The Function Showing Several Level Curves F X Y Y 8x 2 Brainly Com



Example Contour Plots Or Level Curves




Solved Level Curves And Contour Lines Sketch The Contour Chegg Com



Applications Of Gradient The Directional Derivative Suppose We




Contour Plot An Overview Sciencedirect Topics



0 件のコメント:
コメントを投稿